DeepMind Researchers Develop A Machine Learning Technique For Accurate Sampling And Free-Energy Estimate Of Solid Materials Using Normalizing Flows

This Article Is Based On The Research Paper 'Normalizing flows for atomic solids'. All Credit For This Research Goes To The Researchers of This Project 

Please Don't Forget To Join Our ML Subreddit

A significant challenge of computational statistical mechanics is the accurate estimation of equilibrium parameters of a thermodynamic system. For decades, the methods of choice for sampling such systems at large have been molecular dynamics (MD) and hybrid Monte Carlo. Strategies for sampling probability distributions have increased, and most try leveraging normalizing flows.

Normalizing Flows are a technique for creating complicated distributions that involve changing a probability density through a sequence of invertible mappings. These are desirable because of 2 characteristics: first, they can create independent samples rapidly and in parallel, and second, they can offer the precise probability density of their creation method.

Training a flow-based model to approximate a target distribution yields an efficient but approximate sampler, and re-weighting the samples by their probability density can then be used to remove estimation bias for free energy estimation. The exciting part about flows is that they allow us to obtain accurate estimates even without samples from thermodynamic states.

Despite its promise for sampling and free energy estimates of atomistic systems, building and training flow-based models that can compete with current approaches remains a significant issue. One reason is that for simple re-weighting strategies like significance sampling to be accurate in high dimensions, the model must be a very near approximation to the target distribution, which is challenging to create with off-the-shelf approaches.

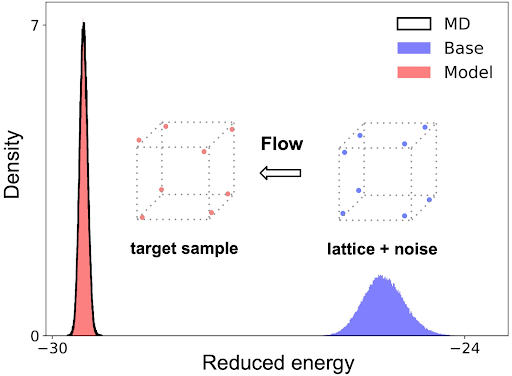
DeepMind proposes a flow model tailored to sampling from atomic solids of identical particles. The model, when trained, approximates the Boltzmann distribution of a chosen solid by adjusting it against a known potential energy function. The training uses only the energy evaluated at model samples and does not require samples from the Boltzmann distribution as ground truth. They can scale it to system sizes of up to 512 particles with excellent approximation quality.

The main aim is to build and train a flow model that can accurately approximate the distribution of atomic solids in particular. They trained a model to approximate the distribution by minimizing a loss function that quantifies the discrepancy between the two. They used the Kullback–Leibler divergence as the loss function.

Targeting specific crystal structures by encoding them into the primary distribution is crucial for their model design. For example, if they want to mimic the hexagonal phase of a crystal, they may change the base distribution’s lattice to hexagonal. Thus, selecting the appropriate base lattice may lead the model toward the desired state without modifying the energy function or relying on ground-truth samples.

Researchers have proved that flow models may simulate single states of interest with high accuracy without training data, laying the groundwork for future research. The computational expense of training is currently a drawback of their suggested strategy. Although producing samples from the model and calculating their probability density is efficient because it can be done in parallel, training the model with gradient-based approaches is intrinsically sequential and slows the process.

With rapid improvements in model architectures, optimizers, and training schemes, it seems likely that this type of approach can be scaled up to more extensive system sizes. The application and adaptation of increasingly suitable normalizing flows is a very active area of research and has immense potential. As outlined in the research paper Normalizing flows for atomic solids, the code in the following repository may be used to train normalizing flow models to create samples of atomic solids.

Paper: https://iopscience.iop.org/article/10.1088/2632-2153/ac6b16/pdf

Github: https://github.com/deepmind/flows_for_atomic_solids